math

Trigonometric Tiling

Playing around with triangles and hexagons, I found an infinite set of trigonometric identities, that fit neatly on a triangle tile.

I didn’t find this trigonometric tiling online, so I decided to share it with everyone.

Definition

For all triangles used in the tiling on this page:

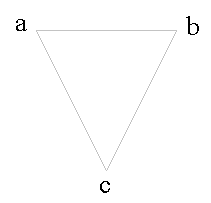
a² + b² = c²

Please note, the points have nothing to do with the triangle lengths or angles. The triangles just provide a neat way of showing all the points.

In all of the tiled triangles below, the top left point squared plus top right point squared equal the bottom point squared.

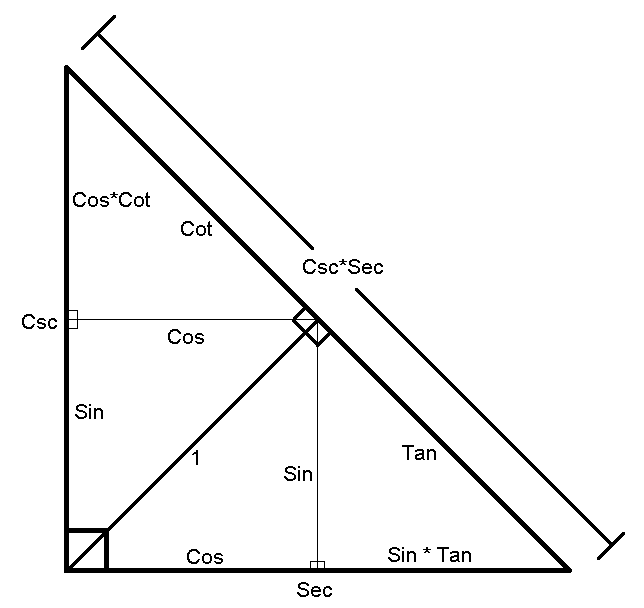
Trigonometric Tile

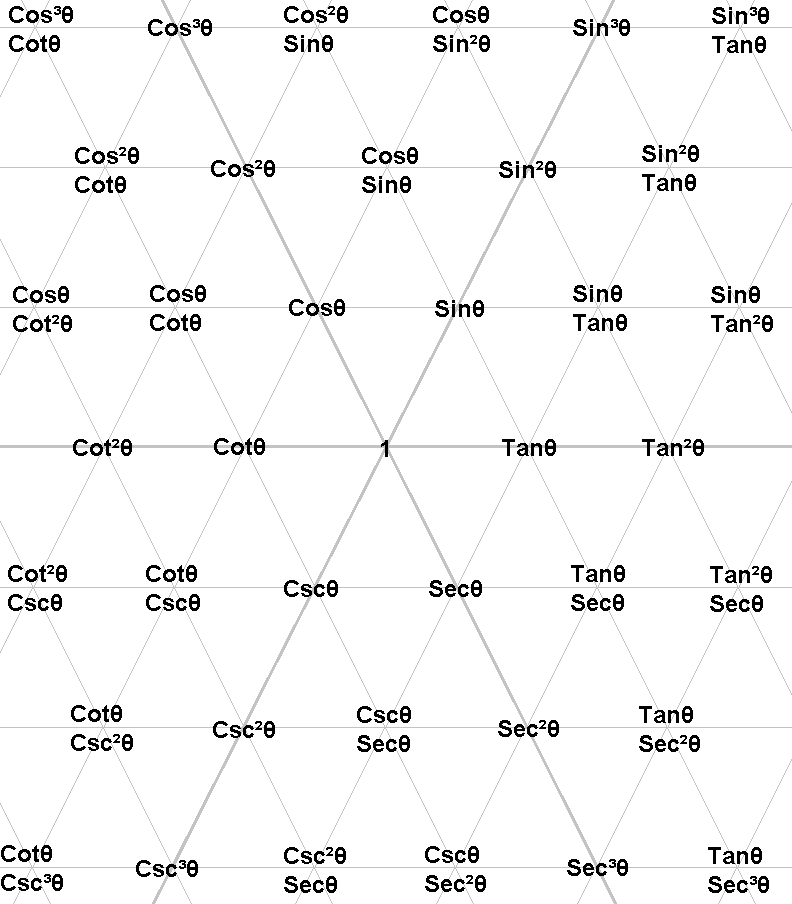
Please read the multiline

as cos θ * sin θ.

Example of identities from tiling

sin²θ + cos²θ = 1

1 + tan²θ = sec²θ

cot²θ + 1 = csc²θ

csc²θ + sec²θ = csc²θ sec²θ

cos²θ sin²θ + sin⁴θ = sin²θ

This trigonometric identity diagram can be extended infinitely in all directions (sin, cos, tan, csc, sec, cot).

Simplified Trigonometric Tile

The tile can be rewritten to use just Sine and Cosine:

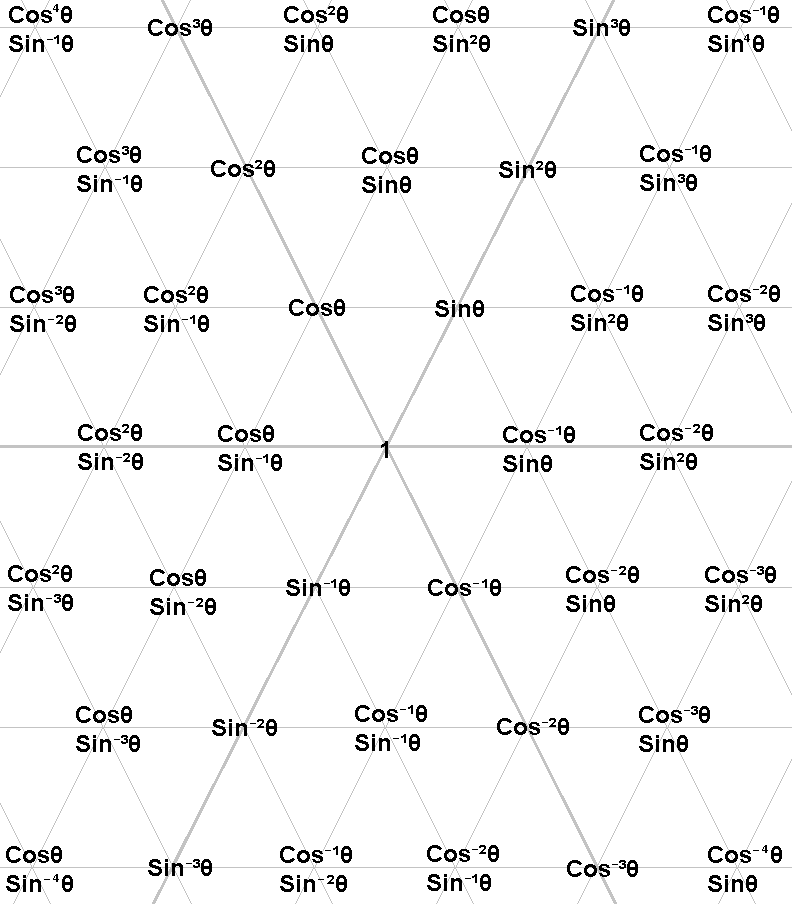
The exponent of each point can be converted from cartesian coordinates for any point:

cos^cθ * sin^sθ

c = (y - x) / 2

s = (y + x) / 2

Proof

The pattern we see in the tiling:

(f(x)^{a + 1} * g(x)^b)² + (f(x)^a * g(x)^{b + 1})² = (f(x)^a * f(x)^b)²

is only true if the following is valid:

f(x)² + g(x)² = 1

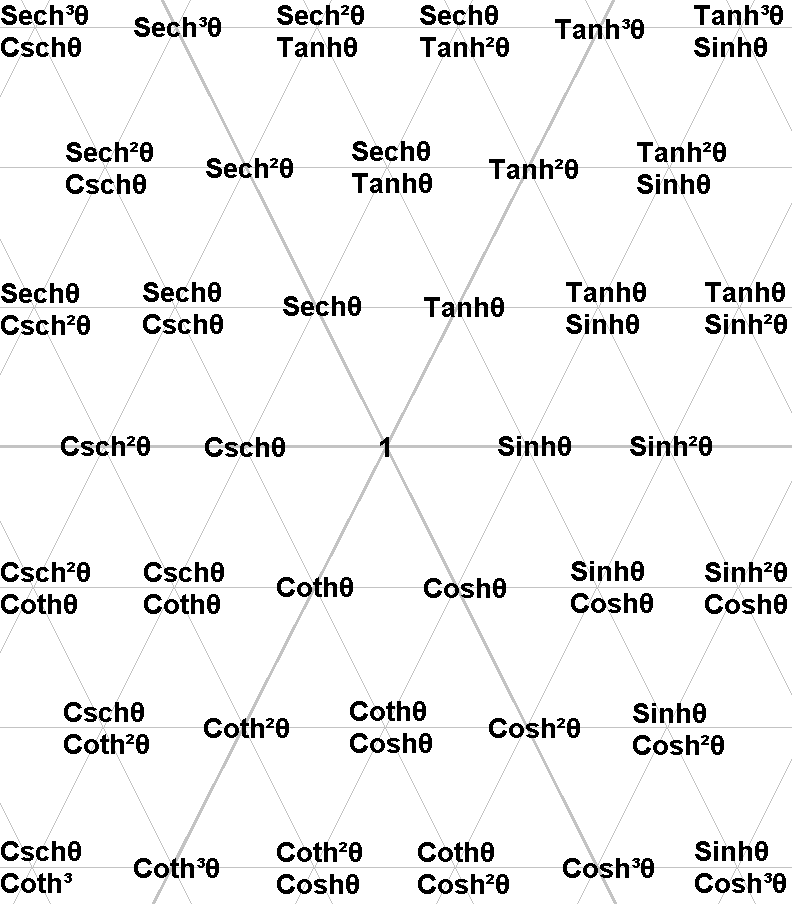
Hence, the tiling can also be doing for hyberbolic functions too.

Hyperbolic Tile

More Properties

Here are a few more useful properties I found..

For all triangles:

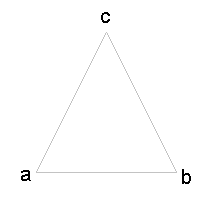
a^-2 + b^-2 = c^-2

---

For all hexagons:

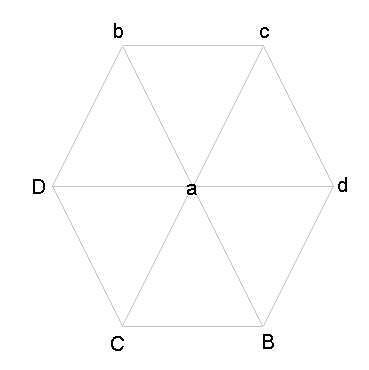
a² = bB = cC = dD

---

For all triangles:

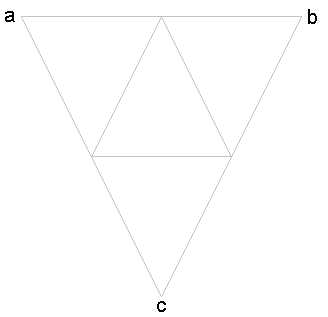
a + b = c

---

For all triangles:

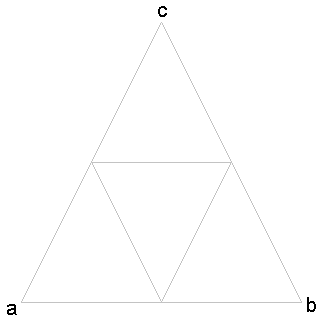
1 / a + 1 / b = 1 / c

Alternative Visual

With all of these triangles using the pythagorean theorem, this information can be represented as an infinite set of triangles. I made a diagram that involves the interesting identities here:

Acknowledgements

I got the idea to build this tiling after watching the video Super Hexagon.

I don’t know who the original author of the “Super Hexagon” is, but it looks like it’s used in some schools as a learning tool to help students with trigonometry.